Anderson localization of elastic waves observed !
Anderson localization of elastic waves observed !
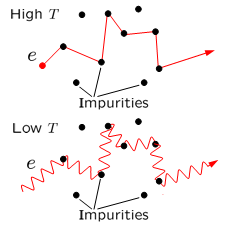 Half a century ago, Philip Anderson proposed electron localization due to disorder as the mechanism that could explain metal-insulator transitions, which had been found to occur with increasing concentration of impurities in a conductor. As he himself later admitted, at the time he did not realize to what extent this idea was going to revolutionize the field of condensed matter physics. In the familiar Drude-Sommerfeld model of electrical conductivity, the electrons are scattered by impurities in a crystal and bounce inside the metal as if they were classical, point-like particles. This model explains why metals have finite electrical resistance, and why, for example, the resistance of a copper wire is proportional to its length. But at low temperatures, quantum interference effects can become important and electrons behave more as waves than as classical particles. Anderson showed that at sufficiently strong disorder, the interferences can start to dominate the transport. In this new regime, the electrons in a disordered material can lose their mobility and the material becomes an insulator.
Half a century ago, Philip Anderson proposed electron localization due to disorder as the mechanism that could explain metal-insulator transitions, which had been found to occur with increasing concentration of impurities in a conductor. As he himself later admitted, at the time he did not realize to what extent this idea was going to revolutionize the field of condensed matter physics. In the familiar Drude-Sommerfeld model of electrical conductivity, the electrons are scattered by impurities in a crystal and bounce inside the metal as if they were classical, point-like particles. This model explains why metals have finite electrical resistance, and why, for example, the resistance of a copper wire is proportional to its length. But at low temperatures, quantum interference effects can become important and electrons behave more as waves than as classical particles. Anderson showed that at sufficiently strong disorder, the interferences can start to dominate the transport. In this new regime, the electrons in a disordered material can lose their mobility and the material becomes an insulator.
Because of its complexity and its many intriguing subtleties, Anderson’s theory was (and still is) the subject of active, and sometimes heated, debates between physicists. The resolution of these debates has suffered from a lack of convincing experimental evidence. After Philip Anderson was awarded the Nobel prize in physics in 1977, localization due to disorder became a true Holy Grail of condensed matter physics. Being essentially an interference phenomenon, Anderson localization is not restricted to electrons but should manifest itself for any type of wave. In the 1980s, the first speculations appeared concerning the possibility of localization for acoustic or electromagnetic waves. From the practical point of view, these “classical” waves are easier to manipulate and to control because their wavelengths are of the order of millimeters or micrometers instead of nanometers for electrons. In addition, contrary to electrons, classical waves do not require low temperatures for these interference effects to occur, and they do not interact with each other. Classical waves are therefore very promising for observation of localization in its “pure” form, i.e. without complications due to the finite, temperature-dependent phase coherence lengths of electrons, their mutual interactions, and scattering from phonons.
 Theory predicts that a true phase transition between extended and localized states can exist only in three dimensions and that it requires rather strong disorder. Observation of this transition with classical waves represents a new challenge for the community of condensed matter physicists. Fabrication of sufficiently disordered samples constitutes the principal difficulty. The most straightforward way of creating a disordered medium is to randomly disperse identical scattering objects in a uniform matrix having different physical properties. The parameters of each object should be adjusted to maximize scattering efficiency. However, properties of a mixture of two (or several) very different components are not easy to predict ! As a consequence, no simple recipe exists to fabricate a “localizing” sample. Recently, considerable efforts have been undertaken to observe Anderson localization of light, but only 2 groups (the group of Prof. Ad Lagendijk in Amsterdam and the group of Prof. Georg Maret in Konstanz) were able to fabricate samples that were sufficiently disordered to exhibit deviations from diffuse behavior. Even though in the case of sound (acoustic and elastic waves) the problem is by no means simpler, we have managed to fabricate strongly disordered samples composed of aluminum beads that are joined together to form a complicated three-dimensional (3D) network. Our ultrasonic experiments show that, in certain frequency ranges, elastic waves in these samples exhibit clear deviations from diffuse behavior.
Theory predicts that a true phase transition between extended and localized states can exist only in three dimensions and that it requires rather strong disorder. Observation of this transition with classical waves represents a new challenge for the community of condensed matter physicists. Fabrication of sufficiently disordered samples constitutes the principal difficulty. The most straightforward way of creating a disordered medium is to randomly disperse identical scattering objects in a uniform matrix having different physical properties. The parameters of each object should be adjusted to maximize scattering efficiency. However, properties of a mixture of two (or several) very different components are not easy to predict ! As a consequence, no simple recipe exists to fabricate a “localizing” sample. Recently, considerable efforts have been undertaken to observe Anderson localization of light, but only 2 groups (the group of Prof. Ad Lagendijk in Amsterdam and the group of Prof. Georg Maret in Konstanz) were able to fabricate samples that were sufficiently disordered to exhibit deviations from diffuse behavior. Even though in the case of sound (acoustic and elastic waves) the problem is by no means simpler, we have managed to fabricate strongly disordered samples composed of aluminum beads that are joined together to form a complicated three-dimensional (3D) network. Our ultrasonic experiments show that, in certain frequency ranges, elastic waves in these samples exhibit clear deviations from diffuse behavior.
 Another difficulty encountered by the groups working on Anderson localization of classical waves was the absence of theoretical model that would be sufficiently accurate and complete to describe realistic experimental situations. It rapidly turned out that such powerful and insightful approaches as the scaling or the self-consistent theories of localization are not sufficient to interpret the shape of the coherent backscattering cone or the time-dependent transmission coefficient measured in experiments. We therefore have proposed and rigorously justified an improved version of the self-consistent theory that features a position-dependent diffusion coefficient. The latter accounts for the finite size of disordered sample and for the inevitable leakage of waves through the sample boundaries. Confrontation of theoretical predictions with existing experimental data suggests that the theory indeed captures the main physics of localization in disordered media of finite size and thus can be used to interpret real experiments.
Another difficulty encountered by the groups working on Anderson localization of classical waves was the absence of theoretical model that would be sufficiently accurate and complete to describe realistic experimental situations. It rapidly turned out that such powerful and insightful approaches as the scaling or the self-consistent theories of localization are not sufficient to interpret the shape of the coherent backscattering cone or the time-dependent transmission coefficient measured in experiments. We therefore have proposed and rigorously justified an improved version of the self-consistent theory that features a position-dependent diffusion coefficient. The latter accounts for the finite size of disordered sample and for the inevitable leakage of waves through the sample boundaries. Confrontation of theoretical predictions with existing experimental data suggests that the theory indeed captures the main physics of localization in disordered media of finite size and thus can be used to interpret real experiments.
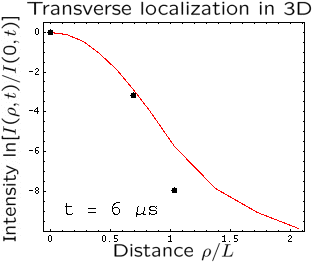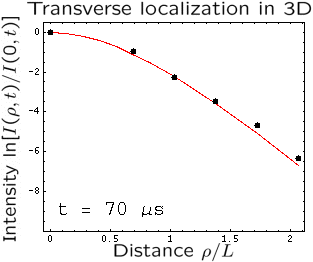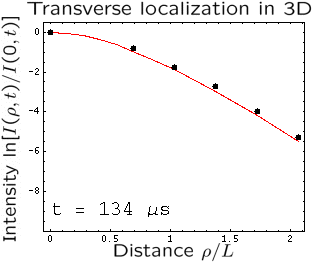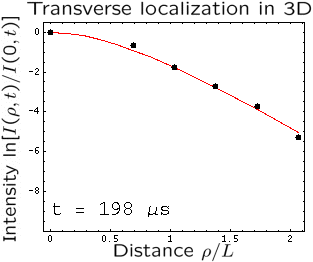 In our paper published in Nature Physics advance online pulblication, 19 October 2008 (DOI 10.1038/nphys1101), we report the comparison of experiments performed using our highly disordered samples with our theoretical model. Our results clearly indicate that Anderson localization of elastic waves takes place in our samples. As an ultimate proof of localization, we propose a new experiment that we call “3D transverse localization”. We illuminate the sample with a short pulse which is tightly focused on one of the sample faces and monitor the time-dependent spatial profile of the transmitted wave intensity on the opposite sample face. In the diffuse regime, the profile widens with time without limits, whereas in the localized regime it “freezes” and does not change any more after a characteristic “localization time” that depends on the sample properties. This time is of the order of 100 microseconds in the animation on the right, where black dots and red lines correspond to experimental data and theory, respectively. Transverse localization is independent of absorption and can be used to measure the localization length which we find to be of the order of 1 cm in our samples.
In our paper published in Nature Physics advance online pulblication, 19 October 2008 (DOI 10.1038/nphys1101), we report the comparison of experiments performed using our highly disordered samples with our theoretical model. Our results clearly indicate that Anderson localization of elastic waves takes place in our samples. As an ultimate proof of localization, we propose a new experiment that we call “3D transverse localization”. We illuminate the sample with a short pulse which is tightly focused on one of the sample faces and monitor the time-dependent spatial profile of the transmitted wave intensity on the opposite sample face. In the diffuse regime, the profile widens with time without limits, whereas in the localized regime it “freezes” and does not change any more after a characteristic “localization time” that depends on the sample properties. This time is of the order of 100 microseconds in the animation on the right, where black dots and red lines correspond to experimental data and theory, respectively. Transverse localization is independent of absorption and can be used to measure the localization length which we find to be of the order of 1 cm in our samples.
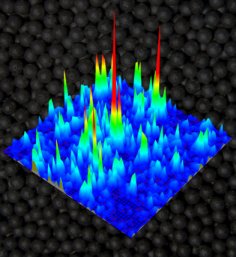 Elastic wave localization in our samples is confirmed by two additional observations : anomalous time-dependent transmission using an extended quasi-plane wave source, and very large statistical fluctuations in the transmitted ultrasonic energy as a function of position and frequency. As in our results on 3D transverse localization, excellent agreement between theory and experiment is found. The simplest way of viewing the large intensity fluctuations is to look at a near-field speckle pattern, which is illustrated in the picture on the left. In the localization regime, the spatial variation of the intensity is dominated by a few intense spikes with little overlap between speckles, in sharp contrast to a typical speckle patterns for diffuse waves. The fluctuations are quantified by the famous dimensionless conductance g, without doubt the most important parameter in mesoscopic physics. The average value of g found for our samples in the localized regime, g = 0.80, is less than 1, demonstrating the localization of waves in accordance with the celebrated criterion for strong localization formulated by David Thouless in the 1970s. This is the first time that all these three different aspects of Anderson localization, transverse confinement of the waves, dynamics in transmission and statistics, have been investigated simultaneously in the same system. All the three measurements convincingly indicate that Anderson localization of elastic waves takes place in our samples.
Elastic wave localization in our samples is confirmed by two additional observations : anomalous time-dependent transmission using an extended quasi-plane wave source, and very large statistical fluctuations in the transmitted ultrasonic energy as a function of position and frequency. As in our results on 3D transverse localization, excellent agreement between theory and experiment is found. The simplest way of viewing the large intensity fluctuations is to look at a near-field speckle pattern, which is illustrated in the picture on the left. In the localization regime, the spatial variation of the intensity is dominated by a few intense spikes with little overlap between speckles, in sharp contrast to a typical speckle patterns for diffuse waves. The fluctuations are quantified by the famous dimensionless conductance g, without doubt the most important parameter in mesoscopic physics. The average value of g found for our samples in the localized regime, g = 0.80, is less than 1, demonstrating the localization of waves in accordance with the celebrated criterion for strong localization formulated by David Thouless in the 1970s. This is the first time that all these three different aspects of Anderson localization, transverse confinement of the waves, dynamics in transmission and statistics, have been investigated simultaneously in the same system. All the three measurements convincingly indicate that Anderson localization of elastic waves takes place in our samples.
H. Hu, A. Strybulevych and J. H. Page
Department of Physics and Astronomy, University of Manitoba, Winnipeg, Manitoba, R3T 2N2 Canada [web page of the laboratory]
S.E. Skipetrov and B.A. van Tiggelen
Université Joseph Fourier, Laboratoire de Physique et Modélisation des Milieux Condensés, CNRS, 25 Rue des Martyrs, BP 166, 38042 Grenoble, France [web page of the laboratory]
When using any material presented on this page, please cite H. Hu, A. Strybulevych, J. H. Page, S.E. Skipetrov and B.A. van Tiggelen, Nature Physics 4, 945 (2008).





